NumPy

Introduction In the realm of numerical integration in Python, SciPy’s integrate.tplquad() function is a triple integration workhorse that solves for the integral of a function of three variables over a rectangular domain. This......

SciPy, a powerful scientific computation library in Python, provides numerous tools for mathematical operations, including integration. This tutorial focuses on the integrate.dblquad() function of SciPy, dedicated to performing double......

Introduction SciPy is a fundamental library for scientific computing in Python, offering a wide range of tools for mathematics, science, and engineering. The integrate.quad_vec() function is a powerful vectorized integrator, enabling......

Welcome to this comprehensive tutorial focused on the integrate.quad() function from the SciPy library. The SciPy integrate module provides several functions for numerical integration, of which quad is most commonly used for......

Introduction The fft.set_global_backend() function in SciPy allows users to set a global FFT backend, empowering them to customize the library’s behavior according to their application’s specific computational needs. This......

Introduction to fft.set_workers() The fft.set_workers() function is a context manager in the SciPy FFT submodule that allows for parallel execution of FFT computations. This is particularly useful when working with large datasets or......

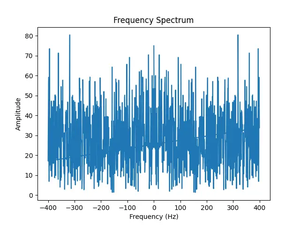
Introduction In the realm of digital signal processing, the Fourier transform is a foundational tool for analyzing the frequencies present in a signal. The fftfreq() function provided by SciPy’s fft module is essential for......

The SciPy library, an essential tool in the Python ecosystem, is widely recognized for its applications in mathematics, engineering, and scientific computing. Specifically, the Fast Fourier Transform (FFT) module within SciPy offers a......

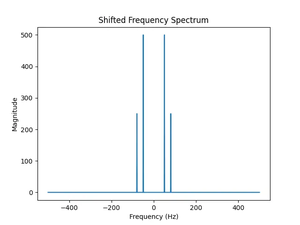
Introduction The fft.fftshift() function in SciPy is a powerful tool for signal processing, particularly in the context of Fourier transforms. It allows for the rearrangement of Fourier Transform outputs into a zero-frequency-centered......

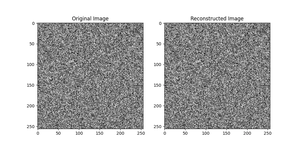
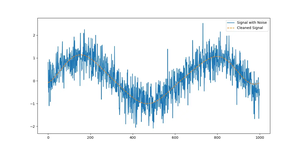
The Fast Fourier Transform (FFT) is a powerful tool for analyzing frequencies in a signal. It is commonly used in various fields such as signal processing, physics, and electrical engineering. Conversely, the Inverse Fast Fourier......

The SciPy library in Python is a core package for scientific computing. It comprises modules for optimization, linear algebra, integration, interpolation, special functions, FFT, signal and image processing, ODE solvers, and more. One of......

When diving into the realm of signal processing or working on relevant application projects, the importance of understanding transformations cannot be overstated. In particular, the Discrete Sine Transform (DST) and its inverse (IDST) are......